exestudiary

Regression modeling with a two-level categorical variable

Suppose that Z is a two-level categorical variable such that Z = A or B.

Define

$$X =  \begin{cases}  1, & \text{if } Z = A \\  0, & \text{otherwise}  \end{cases}$$

Then we can use the following regression model, $$Y = \beta_0 + \beta_1X + \epsilon$$

• $\beta_0 = \mu_B$(called the base line)
• $\beta_1 = \mu_A - \mu_B$
• Consequently, $\beta_0 + \beta_1 = \mu_A$

Since $E(Y) = \beta_0 + \beta_1X$,

if Z = A, X = 1, $E(Y) = \beta_0 + \beta_1 = \mu_A$

if Z = B, X = 0, $E(Y) = \beta_0 = \mu_B$

Suppose that Z is a three-level categorical variable such that Z = A, B or C. 

Define

$X_1 =  \begin{cases}  1, & \text{if } Z = A \\  0, & \text{otherwise}  \end{cases}$

$X_2 =  \begin{cases}  1, & \text{if } Z = B \\  0, & \text{otherwise}  \end{cases}$

Then we can use the following regression model, $$y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \epsilon$$

• $\beta_0 = \mu_C$ (called the base line)
• $\beta_1 = \mu_A - \mu_C$
• $\beta_2 = \mu_B - \mu_C$

Since $E(Y) = \beta_0 + \beta_1X_1 + \beta_2X_2$,

if Z = A, (1, 0), $E(Y) = \beta_0 + \beta_1 = \mu_A$

if Z = B, (0, 1), $E(Y) = \beta_0 + \beta_2 = \mu_B$

if Z = C, (0, 0), $E(Y) = \beta_0 = \mu_C$

Two categorical variables

Consider two categorical variables: One at 3 levels ($F_1, F_2, F_3$) and the other at 2 levels ($B_1, B_2$).

Then, the model can be written as $$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_3 + \epsilon,$$

where

$$X_1 = 1\,if\,F_2\, X_1 = 0, if\,not$$

$$X_2 = 1\,if\,F_3\, X_2 = 0, if\,not$$

$$X_3 = 1\,if\,B_2\, X_3 = 0, if\,not$$

Note that $F_1$ and $B_1$ : base levels

• $\beta_0 = \mu_{11}$ (mean of combination of base levels)
• $\beta_1 = \mu_{2j} - \mu_{1j}$ for any level $B_j$ (j = 1, 2)
• $\beta_2 = \mu_{3j} - \mu_{1j}$ for any level $B_j$ (j = 1, 2)
• $\beta_3 = \mu_{i2} - \mu_{i1}$ for any level $F_i$ (i = 1, 2, 3)

Interaction model with two categorical variables 

Consider an extended model as follows:

$$Y = \beta_0 + \beta_1X_1 + \beta_2X_2 + \beta_3X_3 + \beta_4X_4 + \beta_5X_5 + \epsilon,$$

where 

$$X_1 = 1\,if\,F_2\, X_1 = 0, if\,not$$

$$X_2 = 1\,if\,F_3\, X_2 = 0, if\,not$$

$$X_3 = 1\,if\,B_2\, X_3 = 0, if\,not$$

$$X_4 = X1X3, \, and\, X_5 = X_2X_3$$

Note that $F_1$ and $B_1$ : Base levels.

• $\beta_0 = \mu_{11}$ (mean of combination of base levels)
• $\beta_1 = \mu_{21} - \mu_{11}$ for any level $B_1$ only
• $\beta_2 = \mu_{31} - \mu_{11}$ for any level $B_1$ only
• $\beta_3 = \mu_{12} - \mu_{11}$ for any level $F_1$ only 
• $\beta_4 = (\mu_{22} - \mu_{12}) - (\mu_{21} - \mu_{11})$
• $\beta_5 = (\mu_{32} - \mu_{12}) - (\mu_{31} - \mu_{11})$

Since $F_2$, $B_1$, $\mu_{21} = \beta_0 + \beta_1$ then we can write $\beta_1 = \mu_{21} - \mu_{11}$.

Example(Two categorical variables with interaction)

이걸 보고 우리가 질문할 수 있는 것은 다음과 같습니다. 

1. interaction이 유의한가요?
   • $H_0: \beta_4 = \beta_5 = 0$ vs. $H_1: \beta4 \neq 0\, or\, \beta_5 \neq 0$
   • SAS에서 추가적인 옵션이 test를 걸어줘서 확인을 해도 되나, T-test에서 유추가 가능합니다. 
2. interaction이 없는 모델과 비교할 때는 $R_a^2$을 비교합니다. 

결론: 범주형에 대한 회귀분석을 진행할 때도 interaction을 고려해볼 수 있다는 것입니다. 

Needs for transformations

Transformations are applied to accomplish certain objectives such as 

• to ensure that the model is correctly specified,
• to achieve normality,
• or to stabilize the variance.

Example : Bacteria deaths due to X-ray radiation

$$n_t = \beta_0 + \beta_1 + \epsilon_t$$

9개의 plot 중에 첫 번째 plot을 통해 Lack of fit($E(\epsilon) \neq 0$) 문제를 확인할 수 있습니다.

따라서 X 변환을 통해 이 문제를 해결해주면 좋을 듯 합니다. 

그렇기에 우리가 처음 썼던 식에서 조금 변형을 해주면 다음과 같이 쓸 수 있습니다.

$$n_t = \beta_0 + \beta_1t + \beta_2t^2 + \epsilon_t$$

그런데 첫 번째 그림에서 Lack of fit의 문제는 어느 정도 해결된 듯 보이나 

unequal variance 문제가 발생하였습니다. 

따라서 이 문제를 해결하기 위해 Y 변환을 고려하는 것이 좋을 듯 합니다. 

생물학에서는 Bacteria deaths due to X-ray radiation 문제의 식이 따로 존재합니다. 

$$n_t = n_0 e^{\alpha t}$$

따라서 이 식을 통해 다음과 같은 식을 유도할 수 있습니다.

$$logn_t = log n_0 + \alpha t$$

이 식은 $log n_t$를 Y로 생각하고 $logn_0$를 \beta_0, $\alpha t$를 $\beta_1 X$로 생각하면 선형회귀의 식으로 이해할 수 있습니다. 

따라서 $$logn_t = \beta_0 + \beta_1 t + \epsilon_t$$ 의 값으로 fitting을 하면 

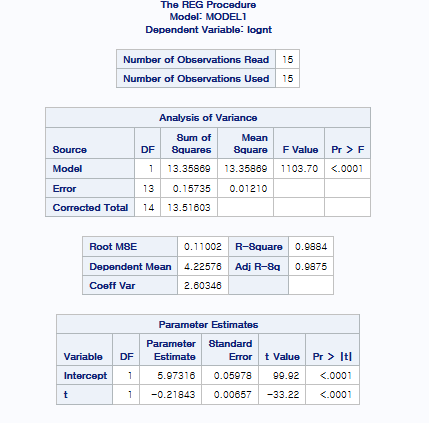
네 이렇게 해서 lack of fit과 unequal variance에 대한 문제를 해결했습니다. 

3번째 그림을 통해 inferential observation을 관찰한 결과, 영향점은 없는 것으로 확인되고 있습니다. 

qqplot을 통해서 Normality도 보장되고 있다는 것을 확인할 수 있습니다. 

그럼 잔차의 독립성을 위해 Durbin-Watson 검정을 시행하면 

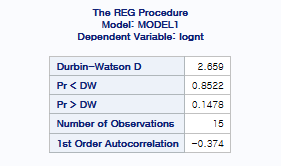
다음과 같이 나옵니다. 

Durbin-Watson D의 값이 2보다 크기 때문에 Pr > DW 부분의 p-value값을 통해 검정을 시행해보면

We fail to reject the null이기에 H0를 기각하지 못합니다.

그렇다고 안 좋은 게 아닙니다. 절대! 

Durbin-Watson 검정은 H0를 기각하지 않아야 잔차의 독립성을 만족한다고 생각하기에 

위의 값을 통해 잔차의 독립성이 만족된다는 것을 확인할 수 있습니다. 

따라서 저희는 이렇게 하여 회귀분석 4가지 가정을 모두 만족시켰습니다. 

또 다른 얘기를 위해 한 가지 예제를 더 들겠습니다. 

Example : Supervisors and supervised workers in industrial establishments

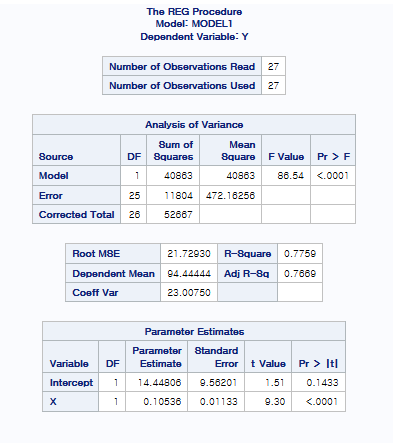
여기서 R-square가 0.7759가 나왔는데 사실 field에 따라 결정계수의 높고 낮음의 기준은 다르기에 field에 따라 결정계수의 값이 높다 나쁘다가 결정됩니다. 

여기서도 마찬가지로 첫 번째 그림에서 Lack of fit과 unequal variance가 의심이 됩니다. 

따라서 X, Y 변환을 고려해야 합니다. 

X의 제곱근을 더해주고, boxcox 변환을 통해 Y변환을 취해 줍니다. 

여기서 만약 선형모형이 맞다고 생각이 들더라도 Lack of fit이 의심되면 2차를 오버피팅하는 습관은 아주 좋습니다.

어차피 선형모형이 맞다고 하면 X의 제곱의 $\hat{\beta}$ = 0 으로 나올 것이기 때문입니다. 

현재 $\lamda$ = 0이 나왔기에 boxcox 변환할 때 log 변환을 취해주고 fitting을 해주면

위와 같은 결과가 나옵니다. 

여기서 그림을 살펴보면 기본 4가지 가정 중 3가지는 만족하는 것으로 보입니다만, 

inferential point가 2개 있는 것을 할 수 있습니다. 

일단 이 결과를 바탕으로 Durbin-Watson 검정을 시행해주면

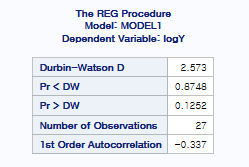
위와 같은 결과가 나오기에 We fail to reject the null 이기에 잔차의 독립성은 만족됩니다.

Sales = $\beta_0$ + $\beta_1$youtube + $\beta_2$facebook + $\beta_3$newspaper + $\epsilon_i$

Q1. Write the assumptions we impose on $\epsilon$
>> $\epsilon$ ~ iid N(0, $\sigma^2$)


Q2. Using the OLS method, estimate regression coefficients.
$\hat{\beta_0}$ = 3.52667
$\hat{\beta_1}$ = 0.04576
$\hat{\beta_2}$ = 0.18853
$\hat{\beta_3}$ = -0.00104


Q3. Estimate $\sigma^2$
4.09096

없으면 root MSE 제곱해서 답 적기($2.02261 ^ 2$)
SSE / DF = MSE


Q4. Test the overall utility of the model.
$H_0: \beta_1 = \beta_2 = \beta_3 = 0$
$H_1: \beta_j \neq 0$ for some j = 1,2,3

Let $\alpha = 0.05$
Since p-value =< 0.0001 is less than $\alpha = 0.05$, we reject $H_0$.
Thus, the overall model is useful.


Q5. Can we claim that the facebook advertising is related to sales? Justify.
$H_0: \beta_2 = 0$
$H_1: \beta_2 \neq 0$

Let $\alpha$ = 0.05.
Since p-value =< 0.0001 is less than $\alpha$ = 0.05, we reject $H_0$.
That is, we can claim that the facebook advertising is related to sales.


Q5-1. Can we claim that the newspaper advertising is related to sales? Justify.
$H_0$: $\beta_3 = 0$
$H_1$: $\beta_3 \neq 0$

Let $\alpha$ = 0.05.
Since p-value = 0.8599 is greater than $\alpha$ = 0.05, we fail to reject $H_0$.
That is, we can claim that the facebook advertising is related to sales.
This means that the newspaper advertising is not related to sales.


Q6. Compute the expected change in the sales when our spending for youtube advertisement increases by 1000달러 while the others are fixed. 
45.76달러(0.04576 * 1000달러)


Q7. Compute the expected sale when we spend 1000달러 for each method of adv.
$\hat{Sale}$
45.76 + 188.53 + 3526.67 - 1.04= 3.7599 * 1000

Q7-1. Compute the expected sale when we spend 0달러 for all of adv.
x들의 값이 0일 때의 기댓값이 위의 질문에 대한 대답
$\beta_0$ => 3.52667 * 1000달러

$\beta_0$는 실제의 데이터 변수의 성질에 따라 x들의 값을 0으로 둘 수 있는지 없는지가 갈린다. 

Q8. Can we argue that youtube is negatively related to the sale?
1. youtube랑 sales와 관계가 있는지부터 확인($\beta$)
2. 그러고 난 다음에 관계가 있으면 $\hat{\beta}$의 값을 신뢰할 수 있음. 
   왜냐하면 $\beta_1$의 값이 0이 아니라고 1번에서 결론지었기 때문에

We conclude that $\beta_1 \neq 0$.
However, since $\hat{\beta_1}$ = 0.04576 is greater than 0, we cannot argue that...

Q8-1. Can we argue that newspaper is negatively related to the sale?
We conclude that $\beta_3$ = 0. We cannot argue that ... 


Q9. Compute the R-squared and interpret it.
$R^2$ = 0.8972

89.72% variability in sales can be explained 
by the fitted model (with youtube, facebook, and newspaper.)


Q9-1. adj. R-squared 도 마찬가지.

(학부생이라 오류가 있을 수 있습니다. 댓글로 정정해서 남겨주시면 감사드리겠습니다.)

단순선형회귀는 input이 하나이고 이 input을 통해 y값을 예측하는 모형입니다.

input이 만약에 여러 개면 Mutiple linear regression이라고 하는데 이 부분은 다음 포스팅 때 다뤄보도록 하겠습니다.

단순선형회귀는 독립변수 하나와 종속변수의 관계를 관측할 수 있게 해주는 설명력이 높은 통계적 방법입니다. 

회귀분석의 첫 단추를 끼우는 만큼 단순선형회귀에 대해 제가 배운 내용을 바탕으로 설명을 해보겠습니다. 

Simple linear regression model

• The response variable $Y$ 와 the predictor variable $X$ 는 $$Y = \beta_0 + \beta_1X + \epsilon$$ , where $\epsilon$ is a random error with $E(\epsilon) = 0$. (Population 수준의 모델)

Simple regression model with the observed data

• The regression model for the observed data is $$y_i = \beta_0 +\beta_1x_i + \epsilon_i,   i = 1, 2, ...., n$$ , where $\epsilon_i$ represents the error in $y_i$.

Parameter estimation

• To estimate the unknown regression coefficients, $\beta_0$ and $\beta_1$, the ordinary least squares(OLS) method is commonly used. 
• From the regression model, we can write $$\epsilon_i = y_i - \beta_0 - \beta_1x_i,  i = 1, 2,.... , n.$$
• We estimate $\beta_0$ and $\beta_1$ by minimizing $$S(\beta_0, \beta_1) = \displaystyle\sum_{i=1}^{n}{(y_i - \beta_0 - \beta_1x_1)^2}$$ >> 가장 오른쪽에 있는 식은 Convex function이어서 미분 최솟값 구하면 됩니다.  

우리가 parameter 값을 구하고 싶은데, 현실은 observed data의 X와 Y값 만을 알고 있는 상태입니다. 

그렇기 때문에 우리는 parameter 값을 추정하는 겁니다.  실제 X값과 Y값을 통해 구할 수 있는데,

추정은 다음과 같은 식을 통해 구할 수 있습니다. 

OLS estimate 

• It can be shown that the estimates of \beta_0 and \beta_1 that minimize $S(\beta_0, \beta_1)$ are given by $$\hat{\beta_1} =  \frac{\sum_{i = 1}^{n}{(y_i - \overline{y})(x_i - \overline{x})}}{\sum_{i = 1}^{n}{(x_i - \overline{x})^2}}$$ and $$\hat{\beta_0} = \overline{y} -  \hat{\beta_1}\overline{x}$$
• $\hat{\beta_0} = \overline{y} -  \hat{\beta_1}\overline{x}$ 증명

• $\hat{\beta_1} =  \frac{\sum_{i = 1}^{n}{(y_i - \overline{y})(x_i - \overline{x})}}{\sum_{i = 1}^{n}{(x_i - \overline{x})^2}}$ 증명

이렇게 하여 $\hat{\beta_0}$ 과 $\hat{\beta_1}$을 구할 수 있는데,

여기서 $\hat{}$ 을 취한 이유는 True 값(추정치가 아닌 값)을 모르고 추정치만 알고 있어서 $\hat{}$을 취했습니다.

Fitted values

• The OLS regression line is obtained as $$\hat{Y} = \hat{\beta_0} + \hat{\beta_1}X$$ .
• The $i$-th fitted value is given by $$\hat{y_i} = \hat{\beta_0} + \hat{\beta_1}x_i,  i = 1, 2, ..., n$$ .
• Example.

이렇게 fitted 했다면 해석은 어떻게 해야 하는지 궁금할 수 있을 것 같은데요... 

그런데 그 전에 $Y = \beta_0 + \beta_1X + \epsilon$ 이 식 양변에 평균을 취하게 되면 다음과 같이 나옵니다.

$$E(Y) = \beta_0 + \beta_1X$$ .

왜 이렇게 나오냐면 $E(\beta_0 + \beta_1X + \epsilon)$ 에서 $\beta_0 + \beta_1X$는 이미 값을 알고 있고 그렇기 때문에 상수로 처리됩니다. 그러면 자연스럽게 $\beta_0 + \beta_1X  + E(\epsilon)$ 이 되고, 회귀분석에서는 $E(\epsilon) = 0$이라고 하는 아주 중요한 가정이 있기에 자연스럽게 $E(Y) = \beta_0 + \beta_1X$ 이 식이 유도가 됩니다. 

Interpertation of coefficients

• Recall that $$E(Y) = \beta_0 + \beta_1X$$ .
  - $\beta_0$ is the expected value of $Y$ when $X = 0$.
  - $\beta_1$ is the amount of increase in the expected value of $Y$ for every one-unit increase inn $X$.
• For example E(minutes) = 4.162 + 15.509 $\times$ Units.
  - The average length of calls is the 4.162 minutes when no component needs to be repaired.
  - The average length of calls increases by 15.509 minutes for each additional component that has to be repaired. 

Test of hypothesis

• In the simple linear regression analysis, the usefulness of the predictor(= X) can be tested by using the following hypothesis test:
  $H_0: \beta_1 = 0   versus   H_1: \beta_1 \neq 0$.
  (X와 Y의 linear relationship을 $\beta_1$을 체크하여 확인할 수 있습니다.)
  (주의할 점: $\hat{\beta_1}$을 이용해서 가설검정을 하는 것이 아닙니다.)
• To this end, we need to further assume that
  
  

이렇게 간단한 식에 4가지의 가정이 들어가있습니다. 중요하기에 반드시 알아두는게 좋다고 합니다.

1. $E(\epsilon_i) = 0$

2. $Var(\epsilon_i) = \sigma^2$

3. $\epsilon_i$ ~ Normal

4. $\epsilon_1, ..... \epsilon_n$ are independent.

T-test

• Under $H_0$ : $\beta_1 = 0$, it can be shown that $$T = \frac{\hat{\beta_1}}{s.e.(\hat{\beta_1})}$$ follows a Student's t distribution with n - 2 degrees of freedom, where $$s.e.(\hat{\beta_1}) = \sqrt{\frac{\sum_{i=1}^{n}{(y_i - \hat{y_i})^2/(n-2)}}{\sum_{i=1}^{n}{(x_i - \overline{x})^2}}}$$ .

Using t-distribution, we can compute the p-value. At significant level $\alpha = 0.05$, we reject $H_0$ if the p-value $\leq$ 0.05. Otherwise, we fail to reject $H_0$.

보통은 모델이 유용하기를 바라기 때문에 귀무가설을 기각하기를 원합니다. 

앞서말한 계수들 뿐만 아니라 $\sigma^2$를 추정하는 것도 중요한데요

바로 error의 변동성을 설명하기 위함입니다.

Estimation of $\sigma^2$

• Define $$e_i = y_i - \hat{y_i}, i = 1, 2, .... , n$$ which are called the residuals.
  이렇게 하는 이유는 $\epsilon_i = y_i - \beta_0 - \beta_1x_i$를 
• We can estimate $\sigma^2$ by using $$\hat{\sigma^2} = \frac{\sum_{i=1}^{n}{e_i^2}}{n - 2} = \frac{\sum_{i=1}{n}{(y_i - \hat{y_i})^2}}{n-2} \equiv$$ MSE, 
  where $\sum_{i=1}{n}{(y_i - \hat{y_i})^2}$ is referred to as SSE (Sum of Squares of Errors) and n -2 is called the df(degrees of freedom).
  여기서 n은 전체 데이터이고 2는 추정치의 개수입니다. 추정치는 $\beta_0, \beta_1$으로 2개가 존재했습니다. 그렇기에 2를 빼주는 것입니다. 

SAS라는 통계 프로그램을 통해서 MSE를 관측할 수 있는데 밑에 그림의 빨간색 부분이 MSE입니다. 

MSE in SAS

Confidence intervals 

• The (1 - $\alpha$) $\times$ 100% confidence intervals (or limits) for $\beta_0 and \beta_1$ are given by $$\hat{\beta_0} \pm t_{n-2,\alpha/2} \times s.e.(\hat{\beta_1})$$ ,
  where $t_{n-2, \alpha/2}$ is the (1 - $\alpha$ / 2) percentile of a t - distribution with n - 2 df

이렇게 신뢰구간도 설정하고 회귀모델을 fitting 했으면 이제 예측을 해봅시다

(예측은 크게 설명력과 예측력으로 구분할 수 있습니다.)

Prediction

• There are two types of predictions:
  1. Prediction of the value of Y given X, i.e., $Y = \beta_0 + \beta_1X + \epsilon$.
  2. Prediction of the mean of Y given X, i.e., $E(Y) = \beta_0 + \beta_1X$.

여기서 하나 알아갈 수 있는 점은 confidence interval은 prediction of the value of Y given X가 넓을 수 밖에 없습니다. 왜냐하면 $\epsilon$, 즉, error가 포함되어 있기 때문입니다. 

• Given $X = x_0$,
  - in the first case, the predicted value is $\hat{y_0} = \hat{\beta_0} + \hat{\beta_1}x_0$.
  - in the second case, the mean response is $\hat{\mu_0} = \hat{\beta_0} + \hat{\beta_1}x_0$.

Prediction intervals

• The (1 - $\alpha$) $\times$ 1000% prediction limits are given by $$\hat{\mu_0} \pm t_{n-2,\alpha/2} \times s.e.(\hat{\mu_0})$$ and $$\hat{y_0} \pm t_{n-2, \alpha/2} \times s.e.(\hat{y_0})$$ ,
  where $$s.e.(\hat{\mu_0}) = \hat{\sigma}\sqrt{\frac{1}{n} + \frac{(x_0 - \overline{x})^2}{\sum_{i=1}^{n}{(x_i -\overline{x})^2}}}$$ and $$s.e.(\hat{y_0}) = \hat{\sigma}\sqrt{1+ \frac{1}{n} + \frac{(x_0 - \overline{x})^2}{\sum_{i=1}^{n}{(x_i -\overline{x})^2}}}$$
  
  (여기서 보면 Expected value와 value 값의 interval을 측정할 때 차이점이 보입니다. 바로 1이 더해졌냐 안 더해졌냐인데요. value값은 아까 Prediction 파트에서 value값의 confidence interval이 넓을 수 밖에 없다고 한 것과 비슷한 매락의 이야기입니다. $\sigma^2$은 $\epsilon$의 분산이고 $\epsilon$만큼 더해진 것을 확인할 수 있습니다. 그렇기에 더 넓은 confidence interval을 가질 수 밖에 없다고 설명한 것입니다.)

Role of $\sigma^2$

• 분산이 크다는 것은 값들이 선에 비교적 가깝지 않고, 분산이 작다는 것은 선에 비교적 선에 가깝다는 얘기입니다. 
• 그러나 분산 즉, $\sigma$의 분산만을 가지고는 선형성을 추론하기에 어려움이 있습니다. 가령, 범위가 다를 때는 $\sigma$의 분산으로 선형성을 추론하면 오류가 발생할 수 있습니다.

그래서 이 상황에서 고안된 것이

Measuring the strength of the linear relationship

• To remedy the limitation of $\sigma^2$, we can propose to use $$\frac{\sigma^2}{Var(Y)}$$ , since it decreases if $\sigma^2$ decreases or $Var(Y)$ increases.
• 우리는 $\sigma^2$의 값을 모르기 때문에 $\sigma^2$의 추정치인 MSE를 사용할 것입니다. 복습을 하자면 $$MSE = \frac{\sum_{i=1}^{n}{(y_i-\hat{y_i})^2}}{n-2}$$ 이고 $Var(Y)$도 모르기 때문에 추정치인 $\hat{Var}(Y)$을 사용할 것입니다. 이것도 다시 remind 하자면 $$\hat{Var}(Y) = \frac{\sum_{i=1}^{n}{(y_i-\overline{y})^2}}{n-1}$$ 입니다. 

여기서 선형성인 것을 나타내주는 지표인 결정계수가 나옵니다.

$R^2$

• To measure the strength of the linear relationship, we define the so-called $R^2$ as follows:
  $$R^2 = 1 - \frac{\sum_{i=1}{n}{(y_i - \hat{y_i})^2}}{\sum_{i=1}{n}{(y_i-\overline{y})^2}} = 1 - \frac{SSE}{SST}$$
  where SST stands for the total sum of squared deviation in $Y$ from its mean.

Property of $R^2$

• It can be shown that $$\displaystyle\sum_{i=1}^{n}{(y_i - \overline{y})^2} = \displaystyle\sum_{i=1}^{n}{(\hat{y_i}-\overline{y})^2} + \displaystyle\sum_{i=1}^{n}{(y_i - \hat{y_i})^2}$$
  where 왼쪽 식에서 첫 번째 식은 SSR(the sum of squares due to regression)으로 불린다.
  That is, $$SST = SSR + SSE$$ .
  
  
• This implies that $$0 \leq R^2 \leq 1$$
  (그 이유는 $R^2  = SSR/SST$ and $0 \leq SSR \leq SST$).