최소제곱 추정 방법
- 개체에서 발생하는 잔차에 제곱을 취하여 합을 구하는 방식
- 큰 절대값 잔차가 발생하지 않도록 회귀직선을 움직임.
- 한 개의 특이점이 회귀직선의 결정에 막중한 영향력을 가짐.
후버의 M-추정
최소제곱 추정은 함수

으로 정의할 떄

를 최소화
그런데 이 추정치가 안정적이지 못한 이유는 함수가 z²에 비례하는 형태이기 때문
따라서 다음의 변형을 고려한다.

|z| < c에서는 원래의 함수와 같지만 그 밖에서는 원래 함수보다 천천히 증가한다.
이를 반영한 후버의 M-추정량은

로 얻어진다.
여기서 σ를 모르기 때문에 (다음 페이지의) MAD로 추정해 사용한다.
MAD (median of absolute deviations)

를 가정하고 σ에 대한 로버스트 추정량으로 IQR / 1.35 를 사용한다.
MAD는 또 다른 로버스트 추정량으로

라 정의한다.
목적함수 l ₀ (z) vs. l ₁ (z)
ell.0 = function(z){z^2}
ell.1 = function(z){c = 1.345; ifelse(abs(z) < c, z^2, c*(2*abs(z) - c))}
z = seq(-6, 6, 0.1)
y.0 = ell.0(z)
y.1 = ell.1(z)
par(mfrow = c(1,2), pty = 's', mar = c(5, 3, 1, 3))
plot(y.0 ~ z, type = "l", lwd = 2, ylim = c(0, 30),
ylab = expression(paste("\u2113")[0](z)))
plot(y.1 ~ z, type = "l", lwd = 2, ylim = c(0, 30),
ylab = expression(paste("\u2113")[1](z)))
par(new = T)
plot(y.0 ~ z, type = "l", lwd = 2, lty = "dotted", ylim = c(0, 30), ylab = "")
코드해석:
1. ell.0과 ell.1은 앞에서 봤던 l ₀, l ₁의 목적함수를 뜻한다.
2. ell.1에서 ifelse는 첫 번째 조건을 만족하면 z² 을 하고 아니면 c * (2 * abs(z) - c)를 한다.
코드결과:

LMS/ LTS 추정
> 자료점을

라 하고, 잔차를

라 할 때, 최소제곱법은

을 풀어 회귀직선을 얻는다.
LMS
> 반면에 LMS (Least Median of Squares) 회귀는 로버스트성의 관점에서 이 목적식을

으로 개량한다.
> 최소제곱법은 Least Squares지만 Least Mean of Squares으로 간주 가능하다.
> LS는 선형대수적 풀이가 가능하지만 LMS는 몬테카를로 반복시행으로 해를 찾는다.
LTS
> LTS (Least Trimmed Squares; 최소절삭제곱) 회귀는

을 풀어서 회귀직선을 얻는다.
> q는 잔차제곱에 대한 순서통계량

에서의 순서
> default는 n의 50%정도에 해당하는 [n/2] + [(p+1)/2]
> n의 75% 정도에 맞추면 추정치의 정확도가 높아진다는 연구결과가 있다.
비교1
library(MASS)
m0 = lm(y ~ x) # 최소제곱추정
m1 = rlm(y ~ x) # 후버의 M-추정
m2 = lqs(y ~ x, method = "lms") # lms
m3 = lqs(y ~ x, method = "lts") # lts
par(mfrow = c(1,1), mar = c(5, 3, 1, 3), pty = 's')
plot(y ~ x, ylim = c(-10, 10), cex = 2, pch = 19, col = 'darkgreen')
abline(m.truth$coefficients, lty = "dotted", lwd = 2)
abline(m0$coefficients, col = "darkcyan", lwd = 2)
abline(m1$coefficients, col = "darkblue", lwd = 2)
abline(m2$coefficients, col = "darkred", lwd = 2)
abline(m3$coefficients, col = "orange", lwd = 2)
여기서 보면 최소제곱추정 (lm)은 이상치에 민감해서 이상치쪽으로 방향이 따라간다는 걸 알 수 있다.
lms, lts, 후버의 m-추정 모두 경향을 잘 따라가고 있다.
다른 예를 통해서 조금 더 자세하게 살펴보자.
비교2
1. X: 1,2,3,... , 10으로 고정
2. Y: Y = 2.5 + 0.5X + ε, ε ~ N(0,1)으로 생성
3. 열번 째 자료점은 (100, -100)으로 수정
- x = 100은 '특이한' 설명변수 값
- x = 100이 정상적인 값이라 했을 때도 y = -100은 특이값 ('회귀' 특이점)
set.seed(1234567)
x = seq(1:10)
y = 2.5 + 0.5*x + rnorm(10, 0, 1)
x[10] = 100
y[10] = -100
par(mar = C(5,3,1,3), pty = 's')
plot(y ~ x, ylim = c(-100, 10), cex = 1, pch = 19, col = 'darkgreen')
abline(m.truth$coefficients, lty = 'dotted', lwd = 2)
후버의 M-추정 vs. LMS
m1 = rlm(y ~ x) # 후버의 M-추정
m2 = lqs(y ~ x, method = "lms") # lms
par(mar = c(5,3,1,3), pty = 's', mfrow = c(1,2))
plot(y ~ x, ylim = c(-100, 10), cex = 1, pch = 19, col = 'darkgreen')
abline(m.truth$coefficients, lty = 'dotted', lwd = 2)
abline(m1$coefficients, col = 'darkblue', lwd = 2)
abline(m2$coefficients, col = 'darkred', lwd = 2)
plot(y ~ x, ylim = c(-100, 10), cex = 1, pch = 19, col = 'darkgreen')
abline(m.truth$coefficients, lty = 'dotted', lwd = 2)
abline(m1$coefficients, col = 'darkblue', lwd = 5)
abline(m2$coefficients, col = 'darkred', lwd = 5)
LMS가 후버의 M-추정에 비해 더 경향을 잘 따라간다.
LTS default vs. LTS quantile = 8
m2a = lqs(y ~ x, method = "lts")
m2b = lqs(y ~ x, method = "lts", quantile = 8)
par(mar = c(5,3,1,3), pty = 's')
plot(y ~ x, xlim = c(0, 10), ylim = c(0, 10), cex = 2, pch = 19, col = "darkgreen")
abline(m.truth$coefficients, lty = 'dotted', lwd = 2)
abline(m1$coefficients, col = 'darkcyan', lwd = 5)
abline(m2$coefficients, col = 'purple', lwd = 5)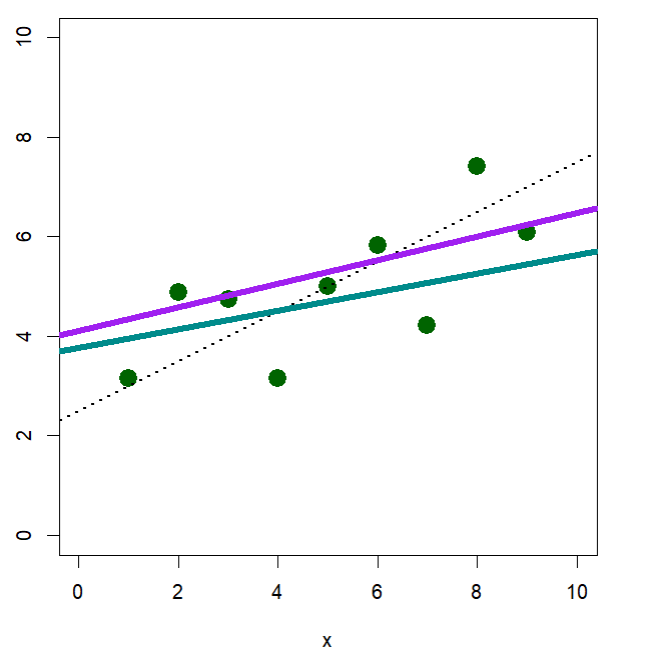
누가 더 경향을 더 잘 따라간다고 할 수는 없다.
'프로그래밍 > R프로그래밍' 카테고리의 다른 글
| EDA - 다중선형회귀 (2) | 2024.05.22 |
|---|---|
| EDA - 줄기와 잎 그림 (0) | 2024.04.08 |
| R프로그래밍 - simulation (2) (1) | 2023.12.05 |
| R프로그래밍 - 중심극한정리 확인 (1) | 2023.12.04 |
| R프로그래밍 - simulation (0) | 2023.12.04 |